Hello, Hallo, Bungiorno, Gruezi, Salve !
Bienvenue sur mon site web, choisissez le thème de votre choix et explorez-le !
Welcome on my website, choose on the theme you want to learn about
Wilkommen auf meiner Webseite, wählen Sie ein Thema und folgen Sie seiner Verbindung!
Je suis directrice d'un département d'ingénierie solution chez THALES Communications & Security, au sein duquel nous réalisons les ingénieries systèmes bout en bout des solutions de communications pour les forces armées : Armée de l'Air, Marine nationale et Armée de Terre. J'y contribue à fournir des solutions modernes et résiliente de communications aux forces, à y insérer les innovations technologiques en ligne avec l'état de l'art, et à développer de manière continue les équipes techniques pour que leur travail soit à la fois passionnant et utile.
Précédemment, j'ai occupé différents rôles de directrice technique, architecte système et responsable de projets toujours autour des solutions de communications radio-mobiles, en particulier dans le domaine aéro-naval militaire, mais aussi pour des usages civils. Mes sujets d'intérêt techniques concernent les enjeux d'architecture et d'optimisation des moyens de transmissions, et vous pourrez trouver plus de détails sur les sujets non-classifiés sur lesquels j'ai travaillé dans l'oblet "Mes travaux".
I am the director of a solution engineering department at THALES Communications & Security, where we carry out end-to-end system engineering communications solutions for the armed forces: Air Force, Navy and Army. In this position, I contribute to provide modern and resilient communications solutions to the forces, to insert technological innovations in line with the state of the art, and to continuously develop the technical teams so that their work is both exciting and useful.
Previously, I have held various roles as technical director, system architect and project manager always around mobile radio communication solutions, in particular in the military air and naval domain, but also for civilian uses. My technical interests are related to the architecture and optimisation of communications systems, and you can find more details on the unclassified topics I have worked on in the "Mes travaux" section.

 IEEE (Senior member)
IEEE (Senior member) SEE
SEEDernière modification : 11 septembre 2022
Last modification: September, 11th, 2022
LES RÉSEAUX DE POINTS : une introduction
Table des matières
1. Introduction
2. Définition et présentation des réseaux de points
2.1 Paramètres fondamentaux
2.2 Performances des réseaux de points sur le canal à bruit additif blanc gaussien
2.3 Performances des réseaux de points sur le canal avec évanouissement de Rayleigh
3. Décodage par sphères
3.1 Décodage par sphères en présence d'un bruit blanc gaussien
3.2 Décodage par sphères en présence d'un évanouissement de Rayleigh
4. Construction des réseaux de points
4.1 Constructions A, B et D
4.2 Les réseaux de Barnes-Wall
5. Décodage à sortie souple des réseaux de points selon le critère MMSE
5.1 Détermination du détecteur à retour de décision (DFE)
5.2 Résultats de simulation
6. Conclusions
1. Introduction
Un réseau de points (lattice) est constitué de centres de sphères empilées possédant une structure de groupe [27]. Utilisés en mathématiques pour les travaux sur les corps finis, les groupes et les formes quadratiques, mais aussi en chimie, où les cristallographes les emploient afin de modéliser le comportement de certains composés chimiques, ils servent également en communications numériques à construire des modulations tant sur le canal à bruit additif blanc gaussien (ou canal AWGN) que sur les canaux à évanouissements (Rice, Rayleigh).
En effet, en utilisant des empilements très denses, il est possible de construire des modulations de grande taille à énergie minimale, permettant ainsi d'effectuer des transmissions à haut débit binaire. Les constellations multidimensionnelles ainsi extraites des réseaux de points connaissent depuis l'apparition des modulations codées au début des années 1980 un grand succès dans le monde des transmissions sur le canal AWGN. Elles ont également été exploitées pour des applications filaires (tels le réseau de Gosset ![]() ou le réseau Leech
ou le réseau Leech ![]() avec lesquels ont été construits des modems [46]). Plus récemment, avec le développement des transmissions radiomobiles pour lesquelles les réseaux performants sur le canal AWGN se sont révélés décevants, on a pu voir l'utilité des réseaux de points à grande diversité, qui permettent de récupérer l'information perdue au cours de la transmission en tirant partie de la redondance liant les composantes d'un point d'un tel réseau.
avec lesquels ont été construits des modems [46]). Plus récemment, avec le développement des transmissions radiomobiles pour lesquelles les réseaux performants sur le canal AWGN se sont révélés décevants, on a pu voir l'utilité des réseaux de points à grande diversité, qui permettent de récupérer l'information perdue au cours de la transmission en tirant partie de la redondance liant les composantes d'un point d'un tel réseau.
Après un rappel des définitions et résultats élémentaires sur les réseaux de points au paragraphe 2, et du fonctionnement du décodage des réseaux de points grâce à l'algorithme de décodage par sphères (Sphere Decoder) au paragraphe ![]() , nous décrirons au paragraphe
, nous décrirons au paragraphe ![]() les méthodes de construction les plus classiques des réseaux de points à partir de codes correcteurs d'erreur, et introduirons les réseaux de Barnes-Wall. Le paragraphe
les méthodes de construction les plus classiques des réseaux de points à partir de codes correcteurs d'erreur, et introduirons les réseaux de Barnes-Wall. Le paragraphe ![]() présentera alors le décodeur DFE de réseaux en grande dimension que nous avons réalisé, ainsi que des résultats de simulation. Finalement nous tirerons quelques conclusions au paragraphe
présentera alors le décodeur DFE de réseaux en grande dimension que nous avons réalisé, ainsi que des résultats de simulation. Finalement nous tirerons quelques conclusions au paragraphe ![]() .
.
2. Définition et présentation des réseaux de points
Un problème fort ancien auxquel les mathématiciens ont été confrontés est celui de déterminer une méthode permettant d'entasser le plus grand nombre de sphères dans un espace donné. La solution, qui serait triviale si il s'agissait de cubes, fut formalisée par Kepler en 1609 avec sa célèbre conjecture, mais ne fut finalement prouvée que tout récemment par Hales [41][57] : il faut, lorsque l'espace est très grand, ranger les boules en couches planes pavées par un motif de triangles équilatéraux pour obtenir l'empilement le plus dense qui soit en dimension ![]() . Dans ce rangement, les centres des sphères constituent un groupe algébrique, appelé réseau cubique à faces centrées (fcc) (ou réseau de Kepler, présenté en figure
. Dans ce rangement, les centres des sphères constituent un groupe algébrique, appelé réseau cubique à faces centrées (fcc) (ou réseau de Kepler, présenté en figure ![]() ). Le volume occupé par les sphères représente alors
). Le volume occupé par les sphères représente alors ![]() de l'espace total.
de l'espace total.
Ce problème de recherche des empilements de sphères optimaux se généralise aisément en dimension supérieure à ![]() , sans qu'il en soit hélàs de même pour la démonstration. Nous allons donc nous intéresser aux réseaux de points de dimension
, sans qu'il en soit hélàs de même pour la démonstration. Nous allons donc nous intéresser aux réseaux de points de dimension ![]() ,
, ![]() entier naturel.
entier naturel.
Les notations suivantes seront utilisées : ![]() est l'ensemble des entiers naturels,
est l'ensemble des entiers naturels, ![]() l'ensemble des entiers relatifs,
l'ensemble des entiers relatifs, ![]() l'ensemble des réels, et
l'ensemble des réels, et ![]() l'espace euclidien réel de dimension
l'espace euclidien réel de dimension ![]() muni de sa distance.
muni de sa distance.
![]() est un vecteur (ou point) de
est un vecteur (ou point) de ![]() si ses composantes
si ses composantes ![]() sont toutes des éléments de
sont toutes des éléments de ![]() . La notation
. La notation ![]() , utilisé sur un vecteur ou une matrice indique la transposition. Pour tout réel
, utilisé sur un vecteur ou une matrice indique la transposition. Pour tout réel ![]() ,
, ![]() est le vecteur de composantes
est le vecteur de composantes ![]() . La norme euclidienne d'un vecteur
. La norme euclidienne d'un vecteur ![]() est notée
est notée ![]() . Une sphère dans
. Une sphère dans ![]() , de rayon
, de rayon ![]() et de centre
et de centre ![]() , est l'ensemble des points
, est l'ensemble des points ![]() vérifiant
vérifiant ![]() .
.
2.1 Paramètres fondamentaux
Nous allons commencer par définir les différents paramètres principaux d'un réseau de points, afin de pouvoir d'une part comprendre ce dont il s'agit, ce que ces réseaux représentent et comment les caractériser. Donnons tout d'abord la définition exacte d'un réseau de points :
Un réseau de points est un sous-groupe discret de rang
Topologiquement, un réseau de points est donc également l'ensemble des vecteurs
![]()
Le réseau, que nous nommerons ![]() sauf indication contraire, peut être vu comme le groupe additif formé par les centres des boules de l'empilement. Par définition d'un groupe additif, le point
sauf indication contraire, peut être vu comme le groupe additif formé par les centres des boules de l'empilement. Par définition d'un groupe additif, le point ![]() appartient à
appartient à ![]() , et de plus la topologie d'un groupe est invariante par toute translation d'un de ses éléments donc il nous suffira toujours d'étudier ce qui se passe autour de l'origine
, et de plus la topologie d'un groupe est invariante par toute translation d'un de ses éléments donc il nous suffira toujours d'étudier ce qui se passe autour de l'origine ![]() pour connaître le comportement autour de tout point de
pour connaître le comportement autour de tout point de ![]() .
.
La famille des
Un sous-réseau de
Un réseau est dit entier s'il est sous-réseau de
Une constellation
Les vecteurs
 |
(1) |
La matrice de Gram
| (2) |
Les éléments ![]() de la matrice de Gram d'un réseau sont les produits scalaires des paires de vecteurs de la base du réseau, à savoir
de la matrice de Gram d'un réseau sont les produits scalaires des paires de vecteurs de la base du réseau, à savoir ![]() . La matrice
. La matrice ![]() est définie positive et symétrique, ses éléments diagonaux étant égaux aux normes au carré des vecteurs de la base.
est définie positive et symétrique, ses éléments diagonaux étant égaux aux normes au carré des vecteurs de la base.
La région de l'espace
Si le parallélotope fondamental d'un réseau n'est pas unique puisqu'il dépend du choix de la base du réseau, le volume fondamental est lui indépendant du choix de la base engendrant ![]() . Dans le cas où
. Dans le cas où ![]() , le volume fondamental est encore égal à la valeur absolue du déterminant de la matrice génératrice
, le volume fondamental est encore égal à la valeur absolue du déterminant de la matrice génératrice ![]() , que l'on note souvent, par abus de langage,
, que l'on note souvent, par abus de langage, ![]() .
.
|
|
La région de l'espace associée à un point
est appelée cellule (ou région) de Voronoï (N.B. : Elle est également parfois nommée cellule de Dirichlet) de
Les cellules de Voronoï d'un réseau pavent donc l'espace euclidien entièrement, remplissant l'espace compris entre les sphères de l'empilement. En figure ![]() -a est présenté en exemple la cellule de Voronoï du réseau à faces cubiques centrées, qui comporte
-a est présenté en exemple la cellule de Voronoï du réseau à faces cubiques centrées, qui comporte ![]() faces. À titre de comparaison, on a représenté en figure
faces. À titre de comparaison, on a représenté en figure ![]() -b le dodécaèdre régulier recouvrant la sphère.
-b le dodécaèdre régulier recouvrant la sphère.
Le réseau étant un groupe additif, on a la propriété de translation des cellules de Voronoï ![]() . Ainsi, toutes les cellules ont-elles le même volume puisqu'elles sont égales (à une translation près) à la cellule de Voronoï de l'origine
. Ainsi, toutes les cellules ont-elles le même volume puisqu'elles sont égales (à une translation près) à la cellule de Voronoï de l'origine ![]() . D'après la structure du réseau, le volume d'une cellule de Voronoï est égal au volume fondamental,
. D'après la structure du réseau, le volume d'une cellule de Voronoï est égal au volume fondamental, ![]() . De plus, le réseau étant géométriquement uniforme [32], chaque cellule de Voronoï est strictement identique aux autres, donc on parlera de "la cellule de Voronoï" du réseau
. De plus, le réseau étant géométriquement uniforme [32], chaque cellule de Voronoï est strictement identique aux autres, donc on parlera de "la cellule de Voronoï" du réseau ![]() .
.
Par la suite, nous ne considérerons que des réseaux engendrés par ![]() vecteurs. La figure
vecteurs. La figure ![]() présente un exemple de réseau en dimension
présente un exemple de réseau en dimension ![]() , à savoir le réseau hexagonal
, à savoir le réseau hexagonal ![]() ainsi que ses différents paramètres élémentaires. Continuons en introduisant des paramètres qui nous permettront de caractériser les performances de nos réseaux de points.
ainsi que ses différents paramètres élémentaires. Continuons en introduisant des paramètres qui nous permettront de caractériser les performances de nos réseaux de points.
Le rayon d'empilement
Les sphères de l'empilement ont toutes le même rayon ![]() . La distance minimale
. La distance minimale ![]() entre les points du réseau est alors donnée par :
entre les points du réseau est alors donnée par :
La densité de remplissage d'un réseau, ou densité
où
Le coefficient d'erreur
La valeur de ![]() ne dépend pas de la sphère considérée en raison de la propriété de translation du réseau.
ne dépend pas de la sphère considérée en raison de la propriété de translation du réseau.
La série theta
où ,
La série theta d'un réseau est une série de variable
2.2 Performances des réseaux de points sur le canal à bruit additif blanc gaussien
Le modèle du système de transmission utilisant une constellation extraite d'un réseau de point est présenté en figure ![]() . Des bits d'informations, générés par une source binaire non représentée, sont étiquetés avant d'être placé en entrée d'un réseau (ou d'une rotation). Ce dernier génère un point
. Des bits d'informations, générés par une source binaire non représentée, sont étiquetés avant d'être placé en entrée d'un réseau (ou d'une rotation). Ce dernier génère un point ![]() du réseau qui est émis sur un canal. Nous considérerons dans ce document deux types de canaux : le canal à bruit additif blanc gaussien et le canal de Rayleigh non sélectif à évanouissements indépendants. En sortie du canal, dont l'état (CSI) est fourni ou estimé par le récepteur, on procède à l'opération de détection et de décodage, d'où on tire les bits décodés. Pour notre calcul de performances, nous considérerons que le décodage suit le critère du maximum de vraisemblance (ML).
du réseau qui est émis sur un canal. Nous considérerons dans ce document deux types de canaux : le canal à bruit additif blanc gaussien et le canal de Rayleigh non sélectif à évanouissements indépendants. En sortie du canal, dont l'état (CSI) est fourni ou estimé par le récepteur, on procède à l'opération de détection et de décodage, d'où on tire les bits décodés. Pour notre calcul de performances, nous considérerons que le décodage suit le critère du maximum de vraisemblance (ML).
Sur le canal à bruit additif blanc gaussien, la probabilité d'erreur par point d'un tel système décroit exponentiellement lorsque le rapport signal à bruit ![]() augmente. Pour une constellation cubique, la probabilité d'erreur est bornée par (voir [86], annexe A.1)
augmente. Pour une constellation cubique, la probabilité d'erreur est bornée par (voir [86], annexe A.1)
 et
et La borne sur la probabilité d'erreur nous conduit à introduire la notion de gain fondamental d'un réseau.
On appelle gain fondamental d'un réseau en dimension
Intéressons nous donc plus à ce gain fondamental ![]() : il est invariant si nous transformons
: il est invariant si nous transformons ![]() par une application composée d'une rotation, d'une symétrie et d'une homothétie : en effet, il est clair que les symétries ou les rotations ne changent pas la distance minimale, ni le volume fondamental. Et par ailleurs, une homothétie de rapport
par une application composée d'une rotation, d'une symétrie et d'une homothétie : en effet, il est clair que les symétries ou les rotations ne changent pas la distance minimale, ni le volume fondamental. Et par ailleurs, une homothétie de rapport ![]() multiplie
multiplie ![]() par
par ![]() et
et ![]() par
par ![]() , ce qui fait que le gain fondamental reste le même.
, ce qui fait que le gain fondamental reste le même.
Lorsque la constellation ![]() a une forme non cubique, le gain de
a une forme non cubique, le gain de ![]() se trouve diminué ou augmenté suivant le moment de second ordre de la constellation. Ce moment d'ordre 2 n'est autre que l'énergie
se trouve diminué ou augmenté suivant le moment de second ordre de la constellation. Ce moment d'ordre 2 n'est autre que l'énergie ![]() (l'énergie moyenne par point) de
(l'énergie moyenne par point) de ![]() . Cette énergie est très liée à la forme de la frontière de
. Cette énergie est très liée à la forme de la frontière de ![]() dans
dans ![]() . On peut donc définir un nouveau gain, dit gain total de la constellation, qui tient compte des caractéristiques fondamentales du réseau
. On peut donc définir un nouveau gain, dit gain total de la constellation, qui tient compte des caractéristiques fondamentales du réseau ![]() et de la forme de la constellation.
et de la forme de la constellation.
Le gain total
Par définition, le gain de forme d'une constellation cubique est égal à 1. La forme sphérique minimise l'énergie moyenne de ![]() en raison de la répartition homogène des distances à l'intérieur d'une hypersphère. Ainsi, le gain de forme
en raison de la répartition homogène des distances à l'intérieur d'une hypersphère. Ainsi, le gain de forme ![]() est-il maximal lorsque
est-il maximal lorsque ![]() possède une forme sphérique. Il s'obtient par le rapport (
possède une forme sphérique. Il s'obtient par le rapport (![]() ) (avec utilisation de l'intégrale de Dirichlet pour le calcul de l'énergie moyenne d'une constellation sphérique [16])
) (avec utilisation de l'intégrale de Dirichlet pour le calcul de l'énergie moyenne d'une constellation sphérique [16])
Le tableau ![]() montre quelques valeurs de
montre quelques valeurs de ![]() pour différentes dimensions. En appliquant la formule de Stirling (
pour différentes dimensions. En appliquant la formule de Stirling (![]() ), on peut montrer que le gain tend en fait vers
), on peut montrer que le gain tend en fait vers ![]() dB lorsque
dB lorsque ![]() tend vers l'infini. On constate donc que le gain de forme est relativement faible comparé au gain fondamental, ce qui explique pourquoi les constellations sphériques, difficiles à réaliser sont peu utilisées et se voient préférer les constellations cubiques. Par la suite, nous ne considérerons dans ce document que ces constellations.
tend vers l'infini. On constate donc que le gain de forme est relativement faible comparé au gain fondamental, ce qui explique pourquoi les constellations sphériques, difficiles à réaliser sont peu utilisées et se voient préférer les constellations cubiques. Par la suite, nous ne considérerons dans ce document que ces constellations.
2.3 Performances des réseaux de points sur le canal avec évanouissement de Rayleigh
Le système de transmission présenté en figure ![]() utilisé sur un canal de Rayleigh admet pour borne supérieure de la probabilité d'erreur par paire, i.e. celle de décoder
utilisé sur un canal de Rayleigh admet pour borne supérieure de la probabilité d'erreur par paire, i.e. celle de décoder ![]() alors que
alors que ![]() a été effectivement émis lorsque l'on fait abstraction des autres points du réseau (voir [86], annexe A.2)
a été effectivement émis lorsque l'on fait abstraction des autres points du réseau (voir [86], annexe A.2)
donc, à haut rapport signal à bruit,
où![]() est la distance produit-
est la distance produit-![]() normalisée entre deux points
normalisée entre deux points ![]() et
et ![]() lorsque ceux-ci différent en
lorsque ceux-ci différent en ![]() composantes.
composantes.
où le facteur de normalisation E correspond à deux points soit ![]() .
.
L'ordre de diversité ou diversité
Utilisant la borne de l'union, on peut donc exprimer la probabilité d'erreur pour une constellation de dimension ![]() extraite du réseau
extraite du réseau ![]() comme
comme
Alors, en remplaçant l'expression de la probabilité d'erreur par paire par sa borne supérieure obtenue dans l'inéquation (![]() ) on obtient
) on obtient
où  , avec
, avec ![]() le nombre de points à distance produit-
le nombre de points à distance produit-![]() de
de ![]() . On notera que la série en
. On notera que la série en ![]() peut être interprétée comme une série theta du réseau, pour peu qu'on considère la distance produit-
peut être interprétée comme une série theta du réseau, pour peu qu'on considère la distance produit-![]() au lieu de la distance euclidienne [79].
au lieu de la distance euclidienne [79].
Asymptotiquement, la borne sur le logarithme de la probabilité d'erreur ![]() décroit linéairement avec une pente
décroit linéairement avec une pente ![]() .
.
3. Décodage par sphères
De nombreux algorithmes existent, spécialisés ou non, permettant de décoder les réseaux de points sur le canal AWGN. Citons à titre d'exemple les travaux de Conway et al. [26], Sun et al. [68], Vardy [75], ou encore l'utilisation de l'algorithme sous-optimal GMD (Generalized minimum distance algorithm [33]). Développés pour le canal gaussien, ces algorithmes reposent principalement sur le décodage souple de codes linéaires, utilisant un treillis ou un calcul sur une valeur de confiance. Applicables au canal de Rayleigh non sélectif, pour lequel les évanouissements multiplient tout simplement les composantes des points émis du réseau, ces algorithmes ne peuvent être utilisés lorsque le réseau est tourné avant de subir l'évanouissement (par application d'une rotation). Dans ce cas, du fait de la corrélation liant les symboles et leurs composantes entre eux, le décodage par étages ou le décodage souple des codes correcteurs d'erreurs ne sont plus possibles.
Le seul algorithme qui reste applicable dans tous les cas est le décodeur universel par sphères [78] reposant sur le critère du maximum de vraisemblance (ML). Il est utilisable aussi bien sur le canal AWGN que sur les canaux à évanouissement de Rayleigh, et sa complexité est indépendante de la taille de la constellation utilisée. Néanmoins, sa complexité limite son utilisation à des dimensions du réseau inférieures ou égales à ![]() . On notera que tout récemment a été proposé une version modifiée de cet algorithme pour le décodage des systèmes d'accès multiple par séquences directes [20][21].
. On notera que tout récemment a été proposé une version modifiée de cet algorithme pour le décodage des systèmes d'accès multiple par séquences directes [20][21].
3.1 Décodage par sphères en présence d'un bruit blanc gaussien
Plaçons nous tout d'abord dans le cas où le canal est à bruit blanc additif gaussien. Le décodage à maximum de vraisemblance d'un réseau de points ![]() quelconque en dimension
quelconque en dimension ![]() utilisé sur ce canal correspond à la recherche, parmi tous les points du réseau, de celui qui est le plus proche du vecteur reçu, soit de celui qui minimise la métrique
utilisé sur ce canal correspond à la recherche, parmi tous les points du réseau, de celui qui est le plus proche du vecteur reçu, soit de celui qui minimise la métrique
L'algorithme de décodage par sphères se limite aux points du réseau ![]() se trouvant dans une sphère de rayon
se trouvant dans une sphère de rayon ![]() centrée sur le point reçu, comme illustré en figure
centrée sur le point reçu, comme illustré en figure ![]() .
.
Le décodeur recherche donc le vecteur ![]() de plus petite norme possible dans le réseau translaté
de plus petite norme possible dans le réseau translaté ![]() de l'espace euclidien
de l'espace euclidien ![]() :
:
Définissons les notations suivantes
Du fait de la présence du bruit sur le canal, les vecteurs ![]() et
et ![]() sont en effet des vecteurs réels. De plus, comme
sont en effet des vecteurs réels. De plus, comme ![]() , on a pour tout indice
, on a pour tout indice ![]()
![]() .
Le point
.
Le point ![]() est un point du réseau dont les coordonnées sont exprimées dans le repère translaté centré sur le point reçu
est un point du réseau dont les coordonnées sont exprimées dans le repère translaté centré sur le point reçu ![]() . On veut que
. On veut que ![]() appartienne à une sphère centrée en
appartienne à une sphère centrée en ![]() (i.e. en
(i.e. en ![]() dans le nouveau repère) et de rayon égal à
dans le nouveau repère) et de rayon égal à ![]() , ce qui nous amène l'inéquation en
, ce qui nous amène l'inéquation en ![]() :
:
Dans ce nouveau système de coordonnées, la sphère de centre ![]() et de rayon au carré égal à
et de rayon au carré égal à ![]() est transformée en un ellipsoïde centré sur l'origine définie par la forme bilinéaire
est transformée en un ellipsoïde centré sur l'origine définie par la forme bilinéaire ![]() . La factorisation de Cholesky de la matrice de Gram
. La factorisation de Cholesky de la matrice de Gram ![]() [25] donne
[25] donne ![]() , où
, où ![]() est une matrice triangulaire supérieure, d'où
est une matrice triangulaire supérieure, d'où
En posant

on obtient
En s'intéressant tout d'abord à ![]() et en poursuivant par les
et en poursuivant par les ![]() , on va déterminer un systèmes de
, on va déterminer un systèmes de ![]() équations déterminant les limites de l'ellipsoïde :
équations déterminant les limites de l'ellipsoïde :
Les bornes données par l'équation (![]() ) nous permettent d'établir la relation générale pour la
) nous permettent d'établir la relation générale pour la ![]() composante
composante ![]() [77][78]
[77][78]



Les bornes trouvées dans les inéquations de la formule (![]() ) nous apprennent que le décodeur par sphères fonctionne avec
) nous apprennent que le décodeur par sphères fonctionne avec ![]() compteurs, 1 pour chacun des nombres
compteurs, 1 pour chacun des nombres ![]() . Il suffit ensuite de faire varier les valeurs des différents compteurs à l'intérieur des bornes trouvées, en tenant compte du fait que celles-ci dépendent des valeurs des autres compteurs. En pratique, ces bornes sont mises à jour de façon récursive [78]. L'intérêt de cette méthode est que les vecteurs dont la norme est supérieure au rayon donné ne seront jamais testés : la complexité de cet algorithme est donc indépendante de la taille de la constellation considérée. Cette méthode permet donc une estimation ML tout en évitant de façon drastique le nombre de points à tester, en particulier lorsque la dimension augmente.
. Il suffit ensuite de faire varier les valeurs des différents compteurs à l'intérieur des bornes trouvées, en tenant compte du fait que celles-ci dépendent des valeurs des autres compteurs. En pratique, ces bornes sont mises à jour de façon récursive [78]. L'intérêt de cette méthode est que les vecteurs dont la norme est supérieure au rayon donné ne seront jamais testés : la complexité de cet algorithme est donc indépendante de la taille de la constellation considérée. Cette méthode permet donc une estimation ML tout en évitant de façon drastique le nombre de points à tester, en particulier lorsque la dimension augmente.
Le choix du rayon de recherche initial ![]() est un point crucial de l'algorithme : afin d'être sûrs de toujours trouver un point du réseau à l'intérieur de la sphère nous devons choisir
est un point crucial de l'algorithme : afin d'être sûrs de toujours trouver un point du réseau à l'intérieur de la sphère nous devons choisir ![]() égal au rayon de recouvrement du réseau. Pour cela, il est par exemple possible de le choisir égal à la borne supérieure de Rogers [27] (p. 40)
égal au rayon de recouvrement du réseau. Pour cela, il est par exemple possible de le choisir égal à la borne supérieure de Rogers [27] (p. 40)
En pratique, on ajuste au fur et à mesure le choix de ![]() , le mettant à jour avec la dernière norme euclidienne calculée pour un point de l'ellipsoïde.
, le mettant à jour avec la dernière norme euclidienne calculée pour un point de l'ellipsoïde.
Enfin on remarquera que, contrairement aux réseaux de points, la constellation utilisée étant finie, des effets de bord pourront apparaître : au cours de la recherche, il ne faudra pas sélectionner les points qui appartiennent au réseau mais pas à la constellation. La complexité de ce test supplémentaire dépend de la forme de la constellation. Par exemple pour les constellations cubiques, il s'agit seulement de vérifier que toutes les composantes du vecteur appartiennent à un certain intervalle.
3.2 Décodage par sphères en présence d'un évanouissement de Rayleigh
Le canal de Rayleigh non sélectif à évanouissements indépendants est une généralisation possible du canal AWGN : il prend en compte la variation de la puissance instantanée reçu et la modélise par des évanouissements indépendants. Le signal reçu s'écrit donc :
Dans ce cas, lorsque le récepteur connait parfaitement l'état du canal (CSI), le décodage ML correspond à la minimisation de la métrique
Soit ![]() la matrice génératrice du réseau
la matrice génératrice du réseau ![]() considéré. Nous pouvons alors définir le réseau
considéré. Nous pouvons alors définir le réseau ![]() de matrice génératrice
de matrice génératrice ![]()
Le nouveau réseau ![]() associé à la matrice
associé à la matrice ![]() peut être vu comme le réseau initial considéré dans un repère dans lequel chaque composante a été multipliée par un facteur
peut être vu comme le réseau initial considéré dans un repère dans lequel chaque composante a été multipliée par un facteur ![]() . Un point de
. Un point de ![]() s'écrit en effet
s'écrit en effet
La métrique à minimiser pour décoder ce réseau est donc, d'après ce qui a été vu au paragraphe précédent,
Ceci signifie [78] que nous pouvons appliquer directement l'algorithme de décodage présenté au paragraphe précédent au réseau ![]() avec pour point reçu
avec pour point reçu ![]() . Le point décodé
. Le point décodé ![]() aura les mêmes composantes entières
aura les mêmes composantes entières ![]() que le point
que le point ![]() .
.
La complexité supplémentaire introduite par les évanouissements vient du fait que pour chaque point reçu il faut travailler avec un nouveau réseau ![]() . Il faut donc effectuer une nouvelle décomposition de Cholesky de la matrice de Gram pour chaque nouveau réseau
. Il faut donc effectuer une nouvelle décomposition de Cholesky de la matrice de Gram pour chaque nouveau réseau ![]() . Il faut également calculer l'inverse de la matrice du réseau
. Il faut également calculer l'inverse de la matrice du réseau ![]()
![]() pour calculer les valeurs des coefficients
pour calculer les valeurs des coefficients ![]() , mais ceci ne demande qu'une opération simple de multiplication puisque la matrice
, mais ceci ne demande qu'une opération simple de multiplication puisque la matrice ![]() peut être précalculée une fois pour toutes.
peut être précalculée une fois pour toutes.
À nouveau, le choix du rayon ![]() est un point crucial : en effet, lorsque la transmission a lieu dans un milieu à forts évanouissements, le choix d'un grand rayon initial impliquera que de nombreux points vont se trouver à l'intérieur de la sphère et donc le décodage pourra être très lent. Pour éviter cet écueil, il est important de pouvoir adapter le choix de
est un point crucial : en effet, lorsque la transmission a lieu dans un milieu à forts évanouissements, le choix d'un grand rayon initial impliquera que de nombreux points vont se trouver à l'intérieur de la sphère et donc le décodage pourra être très lent. Pour éviter cet écueil, il est important de pouvoir adapter le choix de ![]() en fonction des valeurs des coefficients d'évanouissement
en fonction des valeurs des coefficients d'évanouissement ![]() .
.
Ayant à notre disposition un algorithme permettant de décoder les réseaux de points tant sur le canal AWGN que sur le canal de Rayleigh non sélectif, nous allons voir comment construire des réseaux de points performants.
4. Construction des réseaux de points
Les codes correcteurs d'erreurs peuvent servir à construire des empilements de sphères très denses dans l'espace euclidien ![]() [27]. Bien entendu, d'autres méthodes existent, comme la construction par découpage, par couches ou à partir des corps de nombres (voir par exemple [86], chapitre 2). Pour plus de précisions sur ces autres méthodes de construction, on se reportera à l'ouvrage encyclopédique de Conway et Sloane [27]. Nous considérerons ici les différentes méthodes les plus classiques de construction, à partir de codes linéaires binaires, soit la construction A, la construction B et la construction D. On notera que si la construction C n'est pas abordée ici, c'est parce que les empilements qu'elle permet de construire ne sont pas en général des réseaux.
[27]. Bien entendu, d'autres méthodes existent, comme la construction par découpage, par couches ou à partir des corps de nombres (voir par exemple [86], chapitre 2). Pour plus de précisions sur ces autres méthodes de construction, on se reportera à l'ouvrage encyclopédique de Conway et Sloane [27]. Nous considérerons ici les différentes méthodes les plus classiques de construction, à partir de codes linéaires binaires, soit la construction A, la construction B et la construction D. On notera que si la construction C n'est pas abordée ici, c'est parce que les empilements qu'elle permet de construire ne sont pas en général des réseaux.
À titre d'exemple, le tableau ![]() fournit une liste des réseaux de points les plus célèbres [27]. Parmi les plus importants on notera le réseau fcc
fournit une liste des réseaux de points les plus célèbres [27]. Parmi les plus importants on notera le réseau fcc ![]() , le réseau de Schalfli
, le réseau de Schalfli ![]() , le réseau de Gosset
, le réseau de Gosset ![]() , le réseau de Coxeter-Todd
, le réseau de Coxeter-Todd ![]() , le réseau de Barnes-Wall
, le réseau de Barnes-Wall ![]() ou enfin le fameux réseau Leech
ou enfin le fameux réseau Leech ![]() . Les caractéristiques principales de ces réseaux s'y trouvent, et on peut ainsi voir que la densité
. Les caractéristiques principales de ces réseaux s'y trouvent, et on peut ainsi voir que la densité ![]() est une fonction décroissante de la dimension
est une fonction décroissante de la dimension ![]() alors que le coefficient d'erreur
alors que le coefficient d'erreur ![]() en est une fonction croissante.
en est une fonction croissante.
|
4.1 Constructions A, B et D
Construction A
Il s'agit de l'une des méthodes les plus simples de construction d'un réseau de points. Elle repose sur l'utilisation d'un code linéaire ![]() -aire (en pratique, on prend toujours
-aire (en pratique, on prend toujours ![]() ).
).
Il est possible d'interpréter cette construction en utilisant la décomposition binaire d'un entier [16].
On peut alors construire la matrice des coordonnées d'un point ![]() .
.
Soit
Exemple
Considérons le vecteur ![]() . La matrice des coordonnées de
. La matrice des coordonnées de ![]() s'écrit
s'écrit

Un point ![]() appartient donc au réseau défini par construction A si et seulement si sa ligne mod-
appartient donc au réseau défini par construction A si et seulement si sa ligne mod-![]() appartient au code
appartient au code ![]() .
.
Différentes caractéristiques d'un réseau ![]() issu de la construction A à l'aide d'un code linéaire
issu de la construction A à l'aide d'un code linéaire ![]() de longueur
de longueur ![]() , de dimension
, de dimension ![]() et de distance de Hamming minimale
et de distance de Hamming minimale ![]() , noté
, noté ![]() sont aisément calculables,
sont aisément calculables,
| la densité centrée |  |
| le rayon d'empilement |  |
| le coefficient d'erreurs |  |
Lorsque la matrice génératrice du code ![]() est de forme systématique,
est de forme systématique, ![]() , la matrice génératrice du réseau
, la matrice génératrice du réseau ![]() obtenu par construction A est
obtenu par construction A est
Cette construction fournit des réseaux de points efficaces pour des dimensions ![]() . Un exemple de réseaux obtenus par construction A est la famille des réseaux checkerboard, notés
. Un exemple de réseaux obtenus par construction A est la famille des réseaux checkerboard, notés ![]() , obtenus à partir des codes de parité
, obtenus à partir des codes de parité ![]() . Parmi ces réseaux, on notera le réseau fcc
. Parmi ces réseaux, on notera le réseau fcc ![]() et le réseau de Schlafli
et le réseau de Schlafli ![]() . Les réseaux
. Les réseaux ![]() sont les plus denses en dimensions
sont les plus denses en dimensions ![]() seulement. On notera également que les réseaux les plus denses en dimension 6, 7 et 8 soit
seulement. On notera également que les réseaux les plus denses en dimension 6, 7 et 8 soit ![]() ,
, ![]() et
et ![]() s'obtiennent également par construction A.
s'obtiennent également par construction A.
Nous donnons en exemple la matrice du réseau fcc
Construction B
La construction B ajoute une contrainte supplémentaire sur la ligne mod-![]() de la matrice de coordonnées.
de la matrice de coordonnées.
On notera que l'on a ![]() puisque les poids de sont divisibles par 2. De plus, différentes caractéristiques d'un réseau
puisque les poids de sont divisibles par 2. De plus, différentes caractéristiques d'un réseau ![]() issu de la construction A à l'aide d'un code linéaire
issu de la construction A à l'aide d'un code linéaire ![]() sont aisément calculables,
sont aisément calculables,
| la densité centrée |  |
| le rayon d'empilement |  |
| le coefficient d'erreurs |  |
Cette construction est efficace pour des dimensions comprises entre ![]() et
et ![]() . Grâce à cette construction, nous pouvons par exemple obtenir une nouvelle version du réseau
. Grâce à cette construction, nous pouvons par exemple obtenir une nouvelle version du réseau ![]() , mais aussi le réseau
, mais aussi le réseau ![]() (le plus dense en dimension
(le plus dense en dimension ![]() ).
En dimension
).
En dimension ![]() , en utilisant le code de Reed-Muller d'ordre 1 on obtient
, en utilisant le code de Reed-Muller d'ordre 1 on obtient ![]() . On notera que ce réseau est aussi le réseau de Barnes-Wall en dimension
. On notera que ce réseau est aussi le réseau de Barnes-Wall en dimension ![]() , comme nous le verrons au paragraphe
, comme nous le verrons au paragraphe ![]() .
.
Construction D
Généralisant une construction proposée par Barnes et Wall [3], la construction D a été initialement proposée par Barnes et Sloane [4] et s'applique sur une famille de ![]() codes linéaires binaires emboîtés pour produire un réseau dans
codes linéaires binaires emboîtés pour produire un réseau dans ![]() .
.
Soit
Choisissons une base
Le réseau de points
où
On écrit
Le volume fondamental du réseau ![]() , de matrice génératrice
, de matrice génératrice ![]() construite à partir de la base
construite à partir de la base ![]() , est alors donné par
, est alors donné par
Cette construction est une généralisation des constructions A et B. Il suffit en effet de prendre ![]() pour retrouver la construction A et
pour retrouver la construction A et ![]() pour retrouver la construction B. Elle permet quant à elle de construire des réseaux performants en grandes dimensions. On notera que c'est la propriété d'emboitement de ces codes linéaires qui assure que l'empilement obtenu par construction D est un réseau. Les exemples de réseau précédents peuvent donc également être considérés comme des réseaux obtenus par construction D.
pour retrouver la construction B. Elle permet quant à elle de construire des réseaux performants en grandes dimensions. On notera que c'est la propriété d'emboitement de ces codes linéaires qui assure que l'empilement obtenu par construction D est un réseau. Les exemples de réseau précédents peuvent donc également être considérés comme des réseaux obtenus par construction D.
4.2 Les réseaux de Barnes-Wall
Construction des réseaux de Barnes-Wall
Nous allons à présent nous intéresser à une famille particulière de réseaux obtenus par construction D, à savoir les réseaux de Barnes-Wall. En effet, d'après [31], on peut utiliser des codes de Reed-Müller pour construire de nombreux réseaux en suivant les équations suivantes :
où la dimension ![]() est donnée par
est donnée par ![]() et
et ![]() désigne le code de Reed-Müller d'ordre
désigne le code de Reed-Müller d'ordre ![]() et de longueur
et de longueur ![]() .
.
En 1959, Barnes et Wall ont isolé une série de réseaux, appelés ![]() , qui en dimension
, qui en dimension ![]() vérifiaient la propriété suivante :
vérifiaient la propriété suivante :

Il a également été remarqué que les formules des réseaux de Barnes-Wall sont obtenues pour le cas ![]() de la formule générale de construction de réseaux à partir des codes de Reed-Müller. Ainsi obtient-on :
de la formule générale de construction de réseaux à partir des codes de Reed-Müller. Ainsi obtient-on :
Les réseaux de Barnes-Wall ![]() vérifient différentes propriétés bien utiles à qui veut calculer leur gain, densité, ou nombre de voisins (Cf. table
vérifient différentes propriétés bien utiles à qui veut calculer leur gain, densité, ou nombre de voisins (Cf. table ![]() ) :
) :
 |
(42) |
| (43) |
| (44) |
 |
(45) |
|
Construction des codes de Reed-Müller
Les codes de Reed-Müller forment une famille infinie de codes linéaires, introduits en 1954 par Reed et Müller. Ils sont déterminés par deux paramètres ![]() et
et ![]() vérifiant l'inégalité
vérifiant l'inégalité ![]() .
.
![]() représente un code sur
représente un code sur ![]() dont la dimension est égale au nombre de polynômes de degré inférieur ou égal à
dont la dimension est égale au nombre de polynômes de degré inférieur ou égal à ![]() , i.e. i.e.
, i.e. i.e. ![]() . On notera que les codes de Reed-Müller peuvent également être définis comme des codes cycliques étendus [24]. Les caractéristiques du code linéaire binaire
. On notera que les codes de Reed-Müller peuvent également être définis comme des codes cycliques étendus [24]. Les caractéristiques du code linéaire binaire ![]() sont [51] :
sont [51] :
- longueur :

- dimension :

- distance minimum :

On constate par ailleurs que ![]() est le code de Hamming étendu.
est le code de Hamming étendu.
La construction d'un code ![]() consiste à prendre les
consiste à prendre les ![]() vecteurs de composantes
vecteurs de composantes ![]() , choisis de telle façon que
, choisis de telle façon que

On peut alors construire la base du code ![]() comme l'ensemble des combinaisons linéaires des vecteurs
comme l'ensemble des combinaisons linéaires des vecteurs ![]() ,
, ![]() (jusqu'au degré
(jusqu'au degré ![]() ). Donnons un exemple pour
). Donnons un exemple pour ![]() , les
, les ![]() vecteurs de base sont
vecteurs de base sont
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
On notera de plus que par simple permutation de lignes cette matrice est aisément diagonalisable.
Exemple : réseau 
Nous avons déjà vu l'exemple d'un réseau de Barnes-wall avec le réseau ![]() qui n'est autre que
qui n'est autre que ![]() puisque le deuxième code de Reed-Müller permettant de le créer, soit
puisque le deuxième code de Reed-Müller permettant de le créer, soit ![]() n'est autre que le code à répétition en dimension
n'est autre que le code à répétition en dimension ![]() . Donnons ici le réseau de Barnes-Wall en dimension
. Donnons ici le réseau de Barnes-Wall en dimension ![]() , soit
, soit ![]() .
.
5. Décodage à sortie souple des réseaux de points selon le critère MMSE
Le seul algorithme ML de décodage de réseau de points existant, soit l'algorithme de décodage par sphères rappelé au paragraphe ![]() , étant limité pour des raisons de complexité à des dimensions inférieures ou égales à
, étant limité pour des raisons de complexité à des dimensions inférieures ou égales à ![]() , nous proposons un algorithme sous-optimal de décodage permettant de décoder tout réseau
, nous proposons un algorithme sous-optimal de décodage permettant de décoder tout réseau ![]() de dimension inférieure ou égale à
de dimension inférieure ou égale à ![]() sur le canal AWGN et sur le canal de Rayleigh. Cet algorithme repose sur le critère de minimisation de l'erreur quadratique moyenne (critère MMSE). Au lieu de minimiser la distance euclidienne, le décodeur MMSE minimise l'espérance sur l'erreur quadratique dans l'espace
sur le canal AWGN et sur le canal de Rayleigh. Cet algorithme repose sur le critère de minimisation de l'erreur quadratique moyenne (critère MMSE). Au lieu de minimiser la distance euclidienne, le décodeur MMSE minimise l'espérance sur l'erreur quadratique dans l'espace ![]() en entrée du réseau. Nous nous sommes pour cela appuyés sur une première version d'un égaliseur MMSE (employé comme égaliseur à retour de décision (DFE) avec le critère MMSE) présentée dans [60] pour le décodage de matrices de Hadamard et de Fourier sur le canal à évanouissement de Rayleigh. Nous généralisons ici le décodage MMSE à tout réseau réel ou complexe de dimension
en entrée du réseau. Nous nous sommes pour cela appuyés sur une première version d'un égaliseur MMSE (employé comme égaliseur à retour de décision (DFE) avec le critère MMSE) présentée dans [60] pour le décodage de matrices de Hadamard et de Fourier sur le canal à évanouissement de Rayleigh. Nous généralisons ici le décodage MMSE à tout réseau réel ou complexe de dimension ![]() .
.
5.1 Détermination du détecteur à retour de décision (DFE)
L'emploi d'égaliseurs dans les systèmes de communications numériques pour réduire l'interférence entre symboles (IES) est très classique lorsque l'on souhaite effectuer une transmission sur un canal à bande limitée [58]. Lorsque la réponse impulsionnelle du canal est courte, il est possible de réaliser une égalisation selon le critère à maximum de vraisemblance en appliquant par exemple l'algorithme de Viterbi sur le treillis du canal. Dans le cas contraire, la réduction des effets de l'IES est obtenue en utilisant des égaliseurs sous-optimaux mais moins complexes reposant sur le critère de minimisation de l'erreur quadratique moyenne [58].
Bien sûr, on pourra se demander, et à juste titre, la relation entre égalisation et décodage de réseaux de points. Un réseau de points ![]() est un ensemble discret de points dans un espace de dimension
est un ensemble discret de points dans un espace de dimension ![]() ,
, ![]() ou
ou ![]() , obtenu par transformation linéaire du groupe
, obtenu par transformation linéaire du groupe ![]() , c'est-à-dire que l'on a la relation
, c'est-à-dire que l'on a la relation
La figure ![]() montre le modèle du système de transmission ainsi que l'égaliseur à retour de décision qui comprend une matrice aller
montre le modèle du système de transmission ainsi que l'égaliseur à retour de décision qui comprend une matrice aller ![]() et une matrice de retour
et une matrice de retour ![]() . Le vecteur d'entiers
. Le vecteur d'entiers ![]() ayant été placé en entrée du réseau, le vecteur émis est
ayant été placé en entrée du réseau, le vecteur émis est ![]() et le vecteur reçu
et le vecteur reçu ![]() . Le bruit
. Le bruit ![]() sur le canal est additif blanc gaussien de moyenne nulle avec une variance de
sur le canal est additif blanc gaussien de moyenne nulle avec une variance de ![]() par composante. L'entrée du détecteur à seuil, soit la version corrigée par la matrice de retour du vecteur reçu est
par composante. L'entrée du détecteur à seuil, soit la version corrigée par la matrice de retour du vecteur reçu est ![]() et le vecteur estimé, qui est renvoyé en entrée de la matrice de retour
et le vecteur estimé, qui est renvoyé en entrée de la matrice de retour ![]() est noté
est noté ![]() . L'estimation de la
. L'estimation de la ![]() composante n'est pas prise en compte dans le calcul de la matrice de retour pour l'égalisation du
composante n'est pas prise en compte dans le calcul de la matrice de retour pour l'égalisation du ![]() symbole aussi imposons-nous la condition suivante
symbole aussi imposons-nous la condition suivante
On note ![]() la variance par composante du vecteur d'entiers
la variance par composante du vecteur d'entiers ![]() . Nous supposerons par la suite que
. Nous supposerons par la suite que ![]() , ce qui se fait sans perte de généralité puisqu'au besoin il suffit de remplacer
, ce qui se fait sans perte de généralité puisqu'au besoin il suffit de remplacer ![]() par
par ![]() pour garder correctes les équations trouvées. Nous supposons également que
pour garder correctes les équations trouvées. Nous supposons également que ![]() , où
, où ![]() la matrice identité en dimension
la matrice identité en dimension ![]() et
et ![]() est un facteur de corrélation. En pratique, une approximation valable de
est un facteur de corrélation. En pratique, une approximation valable de ![]() est donnée par
est donnée par ![]() . Par conséquent, lorsque le taux d'erreur sur les composantes entières
. Par conséquent, lorsque le taux d'erreur sur les composantes entières ![]() est suffisamment petit,
est suffisamment petit, ![]() . Les notations
. Les notations ![]() ,
, ![]() et
et ![]() représentent respectivement le transposé, le conjugué et le transconjugué de
représentent respectivement le transposé, le conjugué et le transconjugué de ![]() . Enfin toute matrice de la forme
. Enfin toute matrice de la forme ![]() (respectivement
(respectivement ![]() ,
, ![]() ) représente la matrice diagonale dont les composantes sur la diagonale principale sont
) représente la matrice diagonale dont les composantes sur la diagonale principale sont ![]() (respectivement
(respectivement ![]() ).
).
L'égaliseur à retour de décision reposant sur le critère MMSE minimise l'erreur quadratique moyenne (MSE) définie par
Sachant que lors du calcul de l'égaliseur minimisant l'erreur quadratique moyenne, nous prendrons en compte la condition (![]() ) en utilisant les multiplicateurs de Lagrange
) en utilisant les multiplicateurs de Lagrange ![]() . Nous noterons
. Nous noterons ![]() le vecteur formé par ces multiplicateurs.
le vecteur formé par ces multiplicateurs.
La recherche de l'égaliseur minimisant l'expression (![]() ) se fait en la dérivant par rapport aux variables
) se fait en la dérivant par rapport aux variables ![]() et
et ![]() afin d'en déterminer les extrema, soit en déterminant le couple
afin d'en déterminer les extrema, soit en déterminant le couple ![]() vérifiant
vérifiant

Pour cela, nous utilisons les règles rappelées ci-dessous
Nous obtenons alors le système suivant (sans contrainte)
Du système d'équations (![]() ) nous déduisons donc la valeur sans contrainte de
) nous déduisons donc la valeur sans contrainte de ![]()
Il s'agit alors d'introduire ici la contrainte sur les coefficients diagonaux de ![]() donnée par la formule (
donnée par la formule (![]() ), ce qui nous donne l'expression de
), ce qui nous donne l'expression de ![]() avec contrainte
avec contrainte
Nous en déduisons, avec la première ligne du système (![]() ) la valeur de
) la valeur de ![]() avec contrainte
avec contrainte

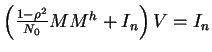 .
.
En remplaçant cette valeur de ![]() dans l'expression de
dans l'expression de ![]() donnée par la formule (
donnée par la formule (![]() ) nous pouvons calculer la valeur des coefficients multiplicateurs de Lagrange permettant de satisfaire la condition (
) nous pouvons calculer la valeur des coefficients multiplicateurs de Lagrange permettant de satisfaire la condition (![]() )
)
Les expressions finales de ![]() et de
et de ![]() sont donc
sont donc
5.2 Résultats de simulation
Le décodeur DFE sous-optimal trouvé au paragraphe précédent est appliqué au décodage d'un réseau dense en grande dimension, le réseau de Barnes-Wall en dimension ![]() sur canal AWGN. L'entrée du filtre de retour est supposée parfaite (ou sans erreur) donc
sur canal AWGN. L'entrée du filtre de retour est supposée parfaite (ou sans erreur) donc ![]() .
.
Le gain fondamental et le coefficient d'erreur du réseau ![]() sont donnés par la table
sont donnés par la table ![]() , soit
, soit ![]() dB et
dB et ![]() respectivement. La valeur de ce gain fondamental nous apprend qu'une constellation finie extraite de ce réseau sera un bon alphabet de canal pour le canal à bruit additif blanc gaussien. En pratique, le gain effectif sera inférieur aux 10.54 dB théoriques du fait du fort coefficient d'erreur
respectivement. La valeur de ce gain fondamental nous apprend qu'une constellation finie extraite de ce réseau sera un bon alphabet de canal pour le canal à bruit additif blanc gaussien. En pratique, le gain effectif sera inférieur aux 10.54 dB théoriques du fait du fort coefficient d'erreur ![]() . L'efficacité spectrale à laquelle nous transmettrons est liée à la structure même du réseau
. L'efficacité spectrale à laquelle nous transmettrons est liée à la structure même du réseau ![]() : si nous reprenons la formule du réseau donnée en formule (
: si nous reprenons la formule du réseau donnée en formule (![]() ), nous avons
), nous avons ![]() , donc pour émettre un point
, donc pour émettre un point ![]() du réseau il nous faudra
du réseau il nous faudra ![]() bits, c'est-à-dire une efficacité spectrale de
bits, c'est-à-dire une efficacité spectrale de ![]() bits par dimension, ou encore
bits par dimension, ou encore ![]() bits par symbole complexe.
bits par symbole complexe.
Afin d'estimer les performances du réseau de Barnes-Wall lui-même, soit son efficacité par rapport au meilleur réseau possible en dimension 256, nous plaçons également sur la figure ![]() une borne des performances optimales sur canal AWGN lorsque la modulation utilisée est un réseau de points en dimension 256, suivant en cela les travaux de Shannon [65].
une borne des performances optimales sur canal AWGN lorsque la modulation utilisée est un réseau de points en dimension 256, suivant en cela les travaux de Shannon [65].
Afin de comparer nos résultats avec la limite que représente le décodage ML, nous allons utiliser l'inégalité (![]() ) qui nous fournit une borne fine sur la probabilité d'erreur par point
) qui nous fournit une borne fine sur la probabilité d'erreur par point ![]() qu'il est possible d'obtenir théoriquement avec un décodeur ML. Nous en déduisons la probabilité d'erreur par bit
qu'il est possible d'obtenir théoriquement avec un décodeur ML. Nous en déduisons la probabilité d'erreur par bit ![]() pour le cas où l'étiquetage utilisé est aléatoire et la probabilité d'erreur par bit
pour le cas où l'étiquetage utilisé est aléatoire et la probabilité d'erreur par bit ![]() pour le cas où l'étiquetage utilisé est un étiquetage de Gray. Les courbes de
pour le cas où l'étiquetage utilisé est un étiquetage de Gray. Les courbes de ![]() et de
et de ![]() sont tracées sur la figure
sont tracées sur la figure ![]() pour
pour ![]() bits par symbole, délimitant la zone hachurée de décodage ML.
Cette efficacité spectrale, proche de
bits par symbole, délimitant la zone hachurée de décodage ML.
Cette efficacité spectrale, proche de ![]() bits par dimension, nous amène à comparer ces résultats avec les performances d'une MAQ-16. La figure
bits par dimension, nous amène à comparer ces résultats avec les performances d'une MAQ-16. La figure ![]() nous montre donc, comme nous l'avions prévu, que le gain pratique est bien inférieur au gain théorique puisqu'il est de
nous montre donc, comme nous l'avions prévu, que le gain pratique est bien inférieur au gain théorique puisqu'il est de ![]() dB.
dB.
Les performances du décodeur à retour de décision reposant sur le critère MMSE sont également présentées sur la figure ![]() lorsqu'utilisé avec une constellation cubique extraite du réseau
lorsqu'utilisé avec une constellation cubique extraite du réseau ![]() . Il est indéniable que le décodage selon le critère MMSE est loin d'atteindre les performances ML sur le canal AWGN. Le décodeur MMSE élimine complètement l'interférence entre symboles générée par la structure du réseau, ce que l'on peut observer en comparant ses performances avec le
. Il est indéniable que le décodage selon le critère MMSE est loin d'atteindre les performances ML sur le canal AWGN. Le décodeur MMSE élimine complètement l'interférence entre symboles générée par la structure du réseau, ce que l'on peut observer en comparant ses performances avec le ![]() à la courbe de la MAQ-16, mais il ne tire aucun avantage de la densité élevée de l'empilement.
à la courbe de la MAQ-16, mais il ne tire aucun avantage de la densité élevée de l'empilement.
 |
6. Conclusions
Après avoir rappelé les notions élémentaires de la théorie des réseaux de points, nous nous sommes intéressés dans ce chapitre à leur décodage, rappelant la technique de décodage par sphères, reposant sur le critère ML mais limitée à de petites dimensions, et proposant un nouvel algorithme de décodage par égalisation à retour de décisions selon le critère sous-optimal de minimisation de l'erreur quadratique moyenne. En effet, le critère à maximum de vraisemblance étant inapplicable pour des dimensions élevées pour des raisons numériques évidentes, le critère MMSE apparaît comme un moyen de résoudre le problème du décodage des réseaux de points en grandes dimensions. Cependant, notre DFE présente des performances décevantes sur le canal à bruit additif blanc gaussien. Le gain fondamental du réseau, provenant de la grande densité du réseau, n'est pas exploité par le critère MMSE qui réalise son optimisation dans l'espace des entiers ![]() et non dans l'espace des points
et non dans l'espace des points ![]() du réseau. Le DFE ne peut en fait que supprimer l'interférence entre symboles générée par le réseau lui-même. Nous restons donc malheureusement bien loin des performances optimales des réseaux, dont Urbanke et Rimoldi [73] ont prouvé récemment qu'ils atteignaient la capacité du canal gaussien dans le cas d'un décodage à maximum de vraisemblance.
du réseau. Le DFE ne peut en fait que supprimer l'interférence entre symboles générée par le réseau lui-même. Nous restons donc malheureusement bien loin des performances optimales des réseaux, dont Urbanke et Rimoldi [73] ont prouvé récemment qu'ils atteignaient la capacité du canal gaussien dans le cas d'un décodage à maximum de vraisemblance.
Dernière modification : 14 décembre 2003
Last modification: Dec., 14th, 2003
Brevets déposés, articles de revue, articles de conférence, chapitres d'ouvrage, contributions en standardisation et congrès sans actes
Divers autres choses ...
1. Liens et manuels utiles
- A not so short introduction to LaTeX (english version), by Tobias Oetiker et al.: format ps, format pdf
- Une courte introduction à LaTeX (version française), par Tobias Oetiker et al.: format dvi, format ps, format pdf
- The TEX catalogue on-line: http://www.ctan.org/tex-archive/help/Catalogue/catalogue.html, alias CTAN. Tout ce qui a de près ou de loin un rapport à LaTeX : packages à jour, documentation, ... s'y trouve. Everything you need about LaTeX is there: up-to-date packages, documents, ...
2. Package Battail
Un petit package sympathique, battail.sty, à ajouter avec \usepackage{battail} en début de fichier. Ce package contient les définitions de différentes variables mathématiques : \bbbn, \bbbr, ... pour représenter les ensembles des entiers naturels, les réels ...
3. Modèle de rapport (pdflatex)
4. Modèle de mémoire de thèse (latex)
5. Installation miktex (latex sous windows)
Vous souhaitez utiliser latex et windows est votre OS ? Moi aussi, et personnellement j'utilise miktex avec Texniccenter. Essayez les !
1. Paramétrer X-Emacs sous Linux
Fichiers de paramétrages (couleurs, modes) pour X-Emacs sous Linux.
2. Introduction à Unix (cours)
Présentation sur Unix : généralités. Même s'il est un peu daté (1997 !) ce cours reste d'actualité pour les principes qu'il brosse.
3. Série de TP sous Unix
TP et exercices pour apprendre à maîtriser Linux/Unix. Allez, essayez :-)
Dernière modification : 4 juillet 2010
Last modification: July, 4th, 2010











![$\displaystyle P_e \leq \tau(\Lambda) Q \left( \sqrt{\frac{d^2_{Emin}}{\sqrt[n/2]{det(\Lambda)}} \frac{E_b}{N_0} \frac{3 \eta}{2^{\eta}} } \right)$](./img_lat/img313.png)
![$\displaystyle \gamma(\Lambda) = \frac{d_{Emin}^2}{\sqrt[n/2]{det(\Lambda)}} = 4 \times \sqrt[n/2]{\delta}$](./img_lat/img316.png)

![$\displaystyle \gamma_s(\mathcal{C})_{max} = \frac{{\vert\vert{\bf x}\vert \vert^... ...grave{e}re}}} = \frac{\pi \times (n+2)}{12 \times \sqrt[n/2]{\Gamma(n/2+1)}} ~.$](./img_lat/img324.png)
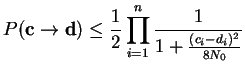











![$\displaystyle \sqrt{C} = \sqrt[n]{ (n\log_e{n} + n \log_e \log_e {n} + 5n) \frac{\sqrt{det(\Lambda)}}{V_n} }$](./img_lat/img389.png)





![$\displaystyle M_{\Lambda_{16}} = \left[ \begin{array}{rrrrrrrrrrrrrrrr} 1 & 1 &... ... & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 4\\ \end{array} \right]$](./img_lat/img489.png)
![$\displaystyle \sum_{i=0}^{a-1} 2^{i} \sum_{j=1}^{k_i} u^{(i)}[j].c_j + 2^a L$](./img_lat/img503.png)



![\begin{displaymath}\begin{array}{l} \hspace{-2cm} M_{BW_{32}}=\\ \hspace{-1cm} ... ... & 0 & 0 & 0 & 0 & 0 & 4\\ \end{array} \right] \\ \end{array}\end{displaymath}](./img_lat/img558.png)




![$\displaystyle \left\{ \begin{array}{l} W M E[{\bf z}{\bf z}^h] M^h + W E[{\bf b... ...at{z}}{\bf\hat{z}}^h] + E[{\bf z}{\bf\hat{z}}^h] = 0 \\ \end{array} \right. ~.$](./img_lat/img598.png)

